Rolling-Cube Mazes
|
The first time one of my rolling-cube mazes appeared was in the May, 1989 issue of Discover (it was in the “Brain Bogglers” section at the back of the magazine). Since then I’ve created many of these mazes and have made a few variations on the basic rules. The following are a sampling of these mazes. The first, “The Very Easy Rolling- Rolling-cube mazes are a precedent to rolling-block mazes. But, of course, rolling- |
|
A Very Easy Rolling-Cube Maze
|
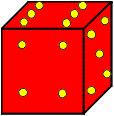
In all these mazes, you must first print out a full- After you’ve printed the diagram, place the die on the square marked Start, and position it so the the 6 is on top and the side with the 4 is facing you (the die should look like the one at the top right of this page). Then tip the die from square to square until you tip it onto the square marked Goal. (You might think of the die as a large carton that is too heavy to turn or slide, but you can tip it over on an edge and have it land in an adjacent square.) You can tip the die onto a square only if the number in the square matches the number on top of the die before it is tipped. However, a square with a large asterisk is a “wild” square. You can move onto one of those squares no matter what number is on top of the die. |
Start |
|
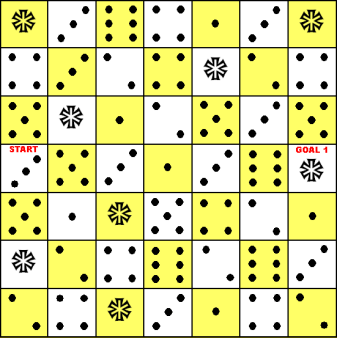
Here is an example: At the start you can only tip the die east onto the square with a 6. A 2 now appears on top, so the next move could be south onto a 2 or east onto a 2. Suppose you go east. A 1 is now on top, so you can only move south. Now a 3 is on top. You can either move south onto the square with a 3 or you can move east onto the square with an asterisk. And so on. In order to tip the die onto the square marked Goal, the die must, of course, have a 3 on top. Click here for the solution. This maze is from my book SuperMazes. |
A Fairly Easy Rolling-Cube Maze
|
This is a maze I created for GAMES Magazine. It ran in the issue of November, 2002. Click here to go to the full-size diagram of the maze and then print it. Place the die on the square marked Start, and position it so the side with the 6 is on top. It doesn’t matter which side is facing you. Then tip the die from square to square until you can land on the square marked Goal. Do not roll onto any of the shaded squares, and (here’s the tricky part) do not roll onto any square if that results in a 1 appearing on top. Here’s an example: Your first move must be one square east. That move is okay (no 1 appears on top). For the second move, try moving east again. Oops! The 1 is now on top, so you have to backtrack one move. Instead, try moving south. That’s okay (there’s no 1). Move south again (okay, still no 1). And so on. By the way, if you make it all the way to Goal but on the last roll a 1 appears, well you haven’t solved the maze. |

|
|
|
A Pretty Difficult Rolling-Cube Maze
 |
This is another maze I created for GAMES Magazine. It ran in the issue of November, 2003. It is based on a maze (with two goals) that first appeared in my book SuperMazes. But the layout here is greatly improved. |
|
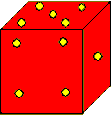
Click here to go to the full-size diagram of this maze and then print it. Place the die on the square marked Start, and position it so the side with the 5 is on top and the side with the 4 is facing you (it should look like the die shown above). This maze uses the same rules of movement as in the Very Easy Rolling-Cube Maze. You can tip the die onto a square if the number in the square matches the number on top of the die before it is tipped. However, a square with a large asterisk is a “wild” square, and you can move onto one of those squares no matter what number is on top of the die. There are two parts to this maze. In Part 1 you roll the die across the maze until you roll it onto Goal 1. In Part 2, begin with the die in whatever position it was in at the end of Part 1 and roll the die back onto the square marked Start (and you need a 3 on top to move onto Start). You must solve both Parts 1 and 2 to solve the maze, and the complete solution takes 58 moves. |
|
|
|
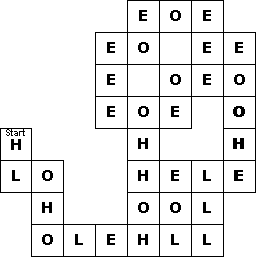
An Impossibly Difficult Rolling-Cube Maze
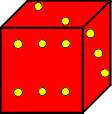 |
Click here to go to the full-size diagram of this maze and then print it. Place the die on the square marked Start, and position it so the side with the 2 is on top and the side with the 6 is facing you (it should look like the die shown at the left). |
|
What you have to do is tip the die off the starting squre; then find a way to get it back onto that square. You can only tip it onto squares that contain letters. The letters stand for low, high, odd, and even. If (and only if) a 1, 2, or 3 is on top of the die, then you can tip it onto a square with an L. If a 4, 5, or 6 is on top, you can tip it onto a square with an H. If a 1, 3, or 5 is on top, you can tip it onto a square with an O. If a 2, 4, or 6 is on top, you can tip it onto a square with an E. I won’t give the solution, but it takes 66 moves. |
|
 |
This maze first appeared in Mad Mazes and later in The Mathemagician and Pied Puzzler (pictured at the left). Here’s how the Mathemagician book came about: In 1993 Tom Rodgers put together a conference of people that Martin Gardner had written about in his Scientific American column. The conference has now become an every-other-year event, called The Gathering for Gardner, and it is now open to anyone involved with recreational mathematics. I’ve already written about that first conference, on another page, since it was where I built my first walk-through logic maze. Everyone at the conference wrote about one of their creations that related to Martin Gardner, and these write-ups were later collected in the Mathemagician book, which was published in 1999. I wrote about this maze, calling it simply “A Maze with Rules.” |
|
Here are the first two paragraphs of what I said: |
|
|
[Here is] one of the mazes from my book. This is my manuscript version of the maze, before my publisher added art work and dopey stories. (Actually, I wrote half the dopey stories and I sort of like some of them.) I chose this particular maze because it illustrates the cross-fertilization that Martin’s columns created. I got the original idea for this maze from remembering columns that Martin wrote in December 1963, November 1965, and March 1975. These columns presented rolling cube puzzles by Roland Sprague and John Harris. The puzzles involved tipping cubes from one square to another on a chess board. As Martin’s columns said, you should think of a cube as a large carton that is too heavy to slide but that can be tipped over on an edge. | |
|
If you want to read the pertinent excerpts from the three columns I mentioned above, you can find them on this page of precedents. | |
|
|
July 27, 2007: New Developments in Rolling Cube Mazes
|
The 19th Canadian Conference on Computational Geometry will be held in Ottawa, Ontario on August You can download the paper by clicking here. It is a 30- |
|
I’m excited to read about a study of rolling cube mazes. However, the “new development” I refer to in the heading of this section is not the study itself. It is a new maze that is presented in the paper. The maze was created by Kevin Buchin, the lead author of the paper, and it came about through an It is my opinion that Buchin’s maze is a revolutionary advance in rolling cube mazes. I’ll explain my reasons for this later, but first you should try the maze. The full-size version of the layout is in a single-page PDF. Click here to load the PDF, then print it (you might have to set Page Scaling to Fit to Printer Margins). The rules are the same as the rules to the Very Easy Rolling-Cube Maze at the top of this page. You place a die on Start, in this case with the 5 on top and the 1 facing you, and you try to roll the die onto Goal. The only obvious difference in this maze is the four large squares at the corners. Roll through these squares in the same way you would roll through the smaller squares. |
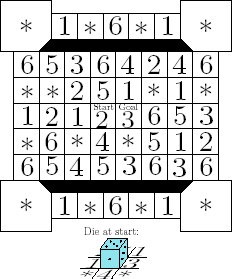
|
|
So: what is so revolutionary about this maze? Well, something happens in it that doesn’t happen in any other rolling cube maze. And that something is—oh, wait, if I write about it here, it might give away the solution. So, after you try the maze, go to Further Discussion of Buchin’s Maze. Actually, it may be that no one will see how this maze is different, but the discussion should make that clear. The discussion also includes a general outline of the solution. |
|
If you ask your browser to print this page, the page will first make some changes and add a few
To the rolling-BLOCK mazes |